문제
https://leetcode.com/problems/longest-common-subsequence/
Longest Common Subsequence - LeetCode
Can you solve this real interview question? Longest Common Subsequence - Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0. A subsequence of a string is a new string genera
leetcode.com
Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.
A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
- For example, "ace" is a subsequence of "abcde".
A common subsequence of two strings is a subsequence that is common to both strings.
Example1
Input: text1 = "abcde", text2 = "ace"
Output: 3
Explanation: The longest common subsequence is "ace" and its length is 3.
Example2
Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.
Example3
Input: text1 = "abc", text2 = "def"
Output: 0
Explanation: There is no such common subsequence, so the result is 0.
설명
주어진 두 문자열에서 공통으로 존재하는 문자열의 길이를 구하는 것이다. LCS(Longest Common Subsequence, 최장 공통부분수열) 알고리즘으로 알려져 있다. 대표적인 DP 문제라고 볼 수 있다.
Longest Common Subsequence 를 보기 전에 Longest Common Substring을 이해하고 가면 좀 더 쉽게 이해할 수 있습니다.
최장 공통 문자열의 경우에는 연속되는 공통 문자열을 구하는 것입니다.
1. 문자열 A와 문자열 B를 한개씩 비교
2. 두 문자가 다르다면 array[i][j]에 0을 표시
3. 두 문자가 같다면 array[i-1][j-1]의 값을 찾아 그 값에 +1
4. 위 과정 반복
점화식
for i in range(len(str_A)):
for j in range(len(str_B)):
if i == 0 or j == 0:
array[i][j] = 0
elif str_A[i] == str_B[j]:
array[i][j] = array[i-1][j-1] + 1
else:
array[i][j] = 0
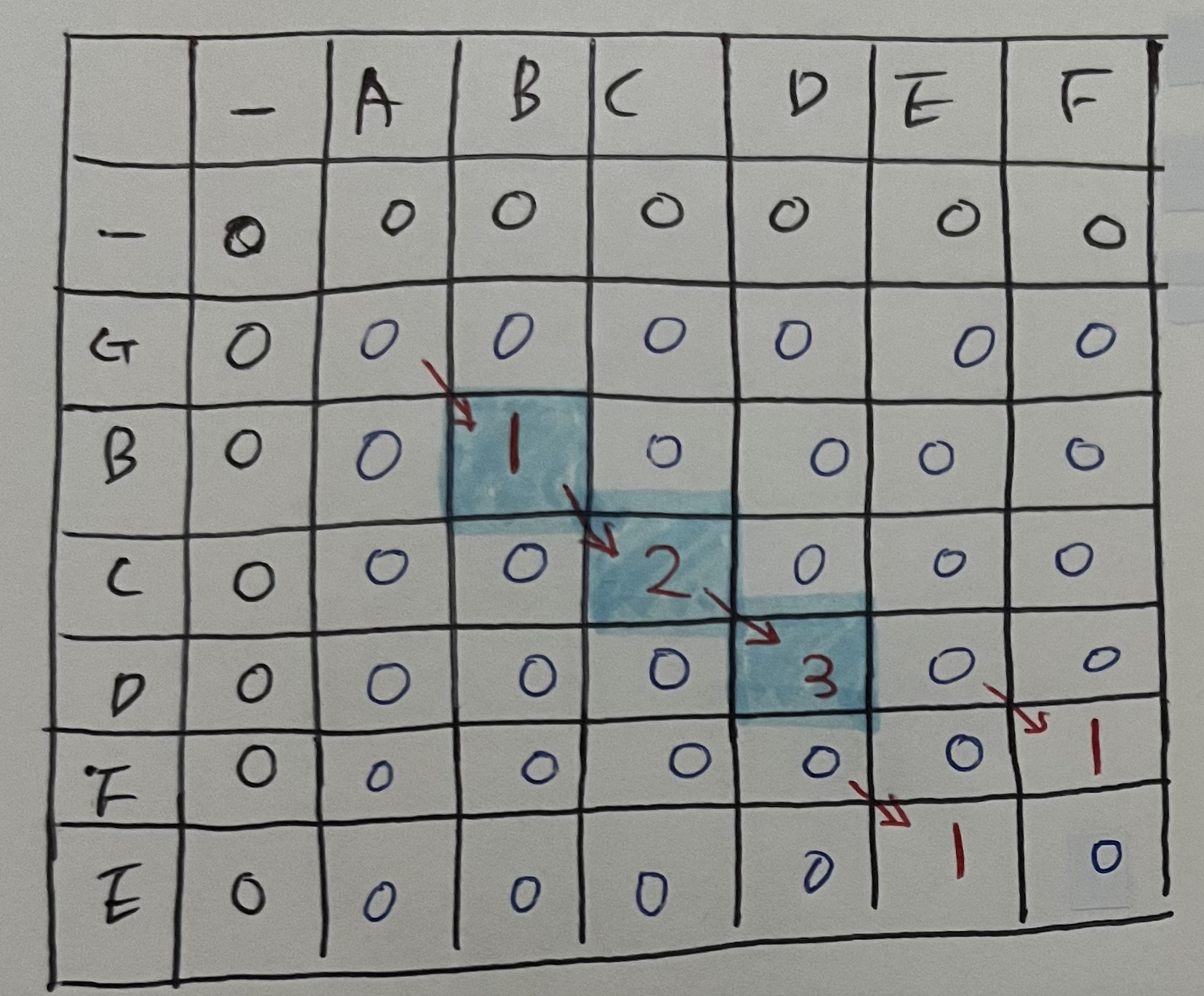
Longest Common Subsequence는 조금 다르다. 부분 수열이기 때문에 같은 문자열이 연속될 필요가 없다.
1. 문자열 A와 문자열 B를 한개씩 비교
2. 두 문자가 다르다면 array[i][j-1] 과 array[i-1][j] 중 큰 값을 표시
3. 두 문자가 같다면 array[i-1][j-1]의 값을 찾아 그 값에 + 1
4. 위 과정 반복
점화식
for i in range(len(str_A)):
for j in range(len(str_B)):
if i == 0 or j == 0:
array[i][j] = 0
elif str_A[i] == str_B[j]:
array[i][j] = array[i-1][j-1] + 1
else:
array[i][j] = max(array[i-1][j], array[i][j-1)
🧐 array[i][j-1]과 array[i-1][j]의 의미
부분수열은 연속된 값이 아니기 때문에 현재의 문자를 비교하는 과정 이전의 최대 공통부분수열은 계속해서 유지되어야 한다. 그 이전의 과정이 바로 array[i][j-1]과 array[i-1][j]이다.
ABCD와 GBCDF를 비교한다고 가정하면
array[i-1][j]의 경우 2 즉, ABC와 GBCDF의 최장 공통부분수열의 값이기 때문에 2이고,
array[i][j-1]의 경우 3 즉, ABCD와 GBCD의 최장 공통부분수열의 값이기 때문에 3이다.
즉, ABCD와 GBCDF의 최장 공통부분수열의 값은 3이된다.
나머지는 위에 Longest Common Substring 알고리즘과 동일하다.
코드
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
len1 = len(text1) + 1
len2 = len(text2) + 1
dp = [[0 for i in range(len2)] for j in range(len1)]
for i in range(1, len1):
for j in range(1, len2):
dp[i][j] = dp[i-1][j-1] + 1 if text1[i-1]==text2[j-1] else max(dp[i-1][j], dp[i][j-1])
return dp[len1-1][len2-1]
결과

'알고리즘 > 동적계획법(DP)' 카테고리의 다른 글
| [LeetCode] 118. Pascal's Triangle | LIM (0) | 2023.05.28 |
|---|---|
| [백준] 18353번: 병사 배치하기 | LIM (0) | 2023.02.05 |
| 동적계획법(DP) (0) | 2021.02.09 |



댓글